爆炸辣

一场回蓝好好玩

T1. 储能表

Description	有一个 n 行 m 列的表格，行从 0 到 n−1 编号，列从 0 到 m−1 编号。每个格子都储存着能量。最初，第 i 行第 j 列的格子储存着 (i xor j) 点能量。所以，整个表格储存的总能量是， 随着时间的推移，格子中的能量会渐渐减少。一个时间单位，每个格子中的能量都会减少 1。显然，一个格子的能量减少到 0 之后就不会再减少了。 也就是说，k 个时间单位后，整个表格储存的总能量是， 给出一个表格，求 k 个时间单位后它储存的总能量。 由于总能量可能较大，输出时对 p 取模。
Input	第一行一个整数 T，表示数据组数。接下来 T 行，每行四个整数 n、m、k、p。
Output	共 T 行，每行一个数，表示总能量对 p 取模后的结果
Sample Input	3 2 2 0 100 3 3 0 100 3 3 1 100
Sample Output	2 12 6
Data Range

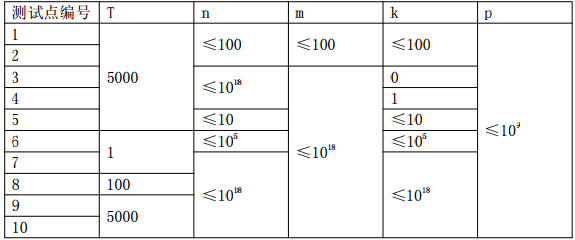传送门：　http://www.lydsy.com/JudgeOnline/problem.php?id=4513

考场一脸懵逼没写数位DP

%%%JHT (n*m)^k竟然拿了20分，自愧不如

#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <cstdlib>
#define NN 5010
#define LL long long
using namespace std;
LL read()
{
	LL xx; bool f=0; char CH;
	for (CH=getchar();CH<'0'||CH>'9';CH=getchar()) if (CH=='-') f=1;
	for (xx=0;CH>='0';CH=getchar()) xx=xx*10+CH-'0'; if (f) xx=-xx;
	return xx;
}
LL ans;
LL p,m,n,k,T;
LL pmax(LL xx){ if (xx<0ll) return 0ll; else return xx;}
int main()
{
	T=read();
	while (T--)
	{
		n=read(), m=read(), k=read(), p=read(), ans=0ll;
		for (LL i=0;i<n;++i)
			for (LL j=0;j<m;++j) ans=(ans+pmax((i^j)-k)%p)%p;
		printf("%lld\n",ans);
	}
	return 0;
}

标算数位DP，代码来自lych_cys

#include<iostream>
#include<cstdio>
#include<cstring>
#define ll long long
#define N 105
using namespace std;

ll n,m,k; int p,lenm,lenn,lenk,len,a[N],b[N],c[N],f[N][2][2][2],g[N][2][2][2],bin[N];
void ad(int &x,int y){ x+=y; if (x>=p) x-=p; }
int main(){
	int cas,i,x,y,z; scanf("%d",&cas);
	while (cas--){
		scanf("%lld%lld%lld%d",&m,&n,&k,&p);
		memset(a,0,sizeof(a)); memset(b,0,sizeof(b)); memset(c,0,sizeof(c));
		lenm=0; for (; m; m>>=1) a[++lenm]=m&1;
		lenn=0; for (; n; n>>=1) b[++lenn]=n&1;
		lenk=0; for (; k; k>>=1) c[++lenk]=k&1;
		len=max(max(lenm,lenn),lenk);
		bin[0]=1; for (i=1; i<=len; i++) bin[i]=(bin[i-1]<<1)%p;
		int i,j,k,l,x,y,z,u,v,tmp;
		memset(f,0,sizeof(f)); memset(g,0,sizeof(g));
		for (x=0; x<2; x++) for (y=0; y<2; y++) for (z=0; z<2; z++)
			for (u=0; u<((x)?2:a[1]); u++)
				for (v=0; v<((y)?2:b[1]); v++)
					if ((u^v)>=c[1] || z){
						ad(f[1][x][y][z],((u^v)-c[1]+p)%p);
						ad(g[1][x][y][z],1);
					}
		for (i=2; i<=len; i++)
			for (x=0; x<2; x++) for (y=0; y<2; y++) for (z=0; z<2; z++)
				for (u=0; u<=max(x,a[i]); u++)
					for (v=0; v<=max(y,b[i]); v++)
						if ((u^v)>=c[i] || z){
							j=x|(u<a[i]); k=y|(v<b[i]); l=z|((u^v)>c[i]);
							tmp=(ll)g[i-1][j][k][l]*((u^v)-c[i])*bin[i-1]%p;
							if (tmp<0) tmp+=p; ad(tmp,f[i-1][j][k][l]);
							ad(f[i][x][y][z],tmp);
							ad(g[i][x][y][z],g[i-1][j][k][l]);
						}
		printf("%d\n",f[len][0][0][0]);
	}
	return 0;
}

T2. 数字配对

Description	有 n 种数字，第 i 种数字是 ai、有 bi 个，权值是 ci。 若两个数字 ai、aj 满足，ai 是 aj 的倍数，且 ai/aj 是一个质数， 那么这两个数字可以配对，并获得 ci×cj 的价值。 一个数字只能参与一次配对，可以不参与配对。 在获得的价值总和不小于 0 的前提下，求最多进行多少次配对。
Input	第一行一个整数 n。 第二行 n 个整数 a1、a2、……、an。 第三行 n 个整数 b1、b2、……、bn。 第四行 n 个整数 c1、c2、……、cn。
Output	一行一个数，最多进行多少次配对
Sample Input	3 2 4 8 2 200 7 -1 -2 1
Sample Output	4
Data Range

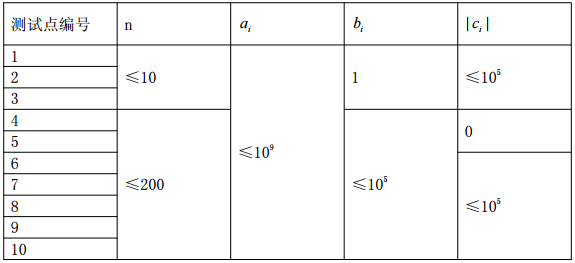传送门：http://www.lydsy.com/JudgeOnline/problem.php?id=4514

唔。。标算写炸只有30分。结果你告诉我tot初值赋错了？！WTF

于是这只兔子就狗带了

像是二分图。。。好像又有费用。那就费用流了呗

听说有许多单纯形AK的大爷%%%

蒟蒻真心QAQ

求拯救

改动一个数字就AK了的程序见下 （辣鸡样例毁我青春

#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <cstdlib>
#include <queue>
#define INF 100000000000000010
#define LL long long
#define NN 1000010
using namespace std;
int tot=1,n,m,a[NN],f[NN],prime[32000],head[NN],S,T,fa[NN];
LL ans=0ll,cost=0ll,b[NN],c[NN],dis[NN];
bool fprime[32100],vis[NN];
queue<int> que;
struct E
{
    int ne,v,u;
    LL w,c;
}e[NN];
int read()
{
    int xx; bool f=0; char CH;
    for (CH=getchar();CH<'0'||CH>'9';CH=getchar()) if (CH=='-') f=1;
    for (xx=0;CH>='0';CH=getchar()) xx=xx*10+CH-'0'; if (f) xx=-xx;
    return xx;
}
LL Read()
{
    LL xx; bool f=0; char CH;
    for (CH=getchar();CH<'0'||CH>'9';CH=getchar()) if (CH=='-') f=1;
    for (xx=0;CH>='0';CH=getchar()) xx=xx*10+CH-'0'; if (f) xx=-xx;
    return xx;
}
void Build(int xx,int yy,LL zz,LL cc)
{
    e[++tot].ne=head[xx], head[xx]=tot, e[tot].v=yy, e[tot].u=xx, e[tot].w=zz, e[tot].c=cc;
    e[++tot].ne=head[yy], head[yy]=tot, e[tot].v=xx, e[tot].u=yy, e[tot].w=0, e[tot].c=-cc;
}
bool SPFA()
{
    while (!que.empty()) que.pop();
    memset(dis,-128,sizeof(dis));
    memset(vis,0,sizeof(vis));
    dis[S]=0, que.push(S), vis[S]=1;
    while (!que.empty())
    {
        int now=que.front(); que.pop();
        vis[now]=0;
        for (int i=head[now];i;i=e[i].ne)
        if (e[i].w && dis[e[i].v]<dis[now]+e[i].c)
        {
            dis[e[i].v]=dis[now]+e[i].c, fa[e[i].v]=i;
            if (!vis[e[i].v]) vis[e[i].v]=1, que.push(e[i].v);
        }
    }
    return dis[T]>=-INF;
}
LL MCF()
{
    LL xx=INF;
    for (int i=fa[T];i;i=fa[e[i].u]) xx=min(xx,e[i].w);
    if (cost+xx*dis[T]<0) xx=-cost/dis[T];
    cost+=xx*dis[T];
    for (int i=fa[T];i;i=fa[e[i].u]) e[i].w-=xx, e[i^1].w+=xx;
    return xx;
}
int Fenjie(int xx)
{
    int total=0,x=xx;
    for (int i=1;i<=prime[0]&&prime[i]<=(int)sqrt(x);++i)
        while (xx%prime[i]==0) xx/=prime[i], ++total;
    if (xx!=1) ++total;
    return total;
}
bool Pri(int xx)
{
    for (int i=1;i<=prime[0]&&prime[i]<=(int)sqrt(xx);++i)
        if (xx%prime[i]==0) return 0;
    return 1;
}
int main()
{
    n=read(), S=n+1, T=n+2;
    memset(fprime,0,sizeof(fprime));
    memset(prime,0,sizeof(prime));
    fprime[1]=1;
    for (int i=2;i<=32000;++i)
    {
        if (!f[i]) prime[++prime[0]]=i;
        for (int j=1;prime[j]*i<=n&&j<=prime[0];++j)
        { fprime[prime[j]*i]=1; if (i%prime[j]==0) break;}
    }
    for (int i=1;i<=n;++i) a[i]=read();
    for (int i=1;i<=n;++i) b[i]=Read();
    for (int i=1;i<=n;++i) c[i]=Read();
    for (int i=1;i<=n;++i) f[i]=Fenjie(a[i])&1;
    for (int i=1;i<=n;++i)
        if (f[i]) Build(S,i,b[i],0); else Build(i,T,b[i],0);
    for (int i=1;i<=n;++i)
    {
        for (int j=i+1;j<=n;++j)
            if (f[i]^f[j])
            {
                if (a[i]%a[j]==0 && Pri(a[i]/a[j]))
                    if (f[i]&1) Build(i,j,INF,c[i]*c[j]);
                    else Build(j,i,INF,c[i]*c[j]);
                else
                if (a[j]%a[i]==0 && Pri(a[j]/a[i]))
                    if (f[i]&1) Build(i,j,INF,c[i]*c[j]);
                    else Build(j,i,INF,c[i]*c[j]);
            }
    }
    while (SPFA())
    {
        LL tmpp=MCF();
        if (tmpp==0ll) break;
        ans+=tmpp;
    }
    printf("%lld\n",ans);
    return 0;
}

T3. 游戏

Description	Alice 和 Bob 在玩一个游戏。 游戏在一棵有 n 个点的树上进行。最初，每个点上都只有一个数字，那个数字是 123456789123456789。 有时，Alice 会选择一条从 s 到 t 的路径，在这条路径上的每一个点上都添加一个数字。对于路径上的一个点 r， 若 r 与 s 的距离是 dis，那么 Alice 在点 r 上添加的数字是 a×dis+b。有时，Bob 会选择一条从 s 到 t 的路径。 他需要先从这条路径上选择一个点，再从那个点上选择一个数字。 Bob 选择的数字越小越好，但大量的数字让 Bob 眼花缭乱。Bob 需要你帮他找出他能够选择的最小的数字。
Input	第一行两个数字 n、m，表示树的点数和进行的操作数。 接下来 n−1 行，每行三个数字 u、v、w，表示树上有一条连接 u、v 的边，长度是 w。 接下来 m 行。每行第一个数字是 1 或 2。 若第一个数是 1，表示 Alice 进行操作，接下来四个数字 s、t、a、b。 若第一个数是 2，表示 Bob 进行操作，接下来四个数字 s、t。
Output	每当 Bob 进行操作，输出一行一个数，表示他能够选择的最小的数字
Sample Input	3 5 1 2 10 2 3 20 2 1 3 1 2 3 5 6 2 2 3 1 2 3 -5 -6 2 2 3
Sample Output	123456789123456789 6 -106
Data Range

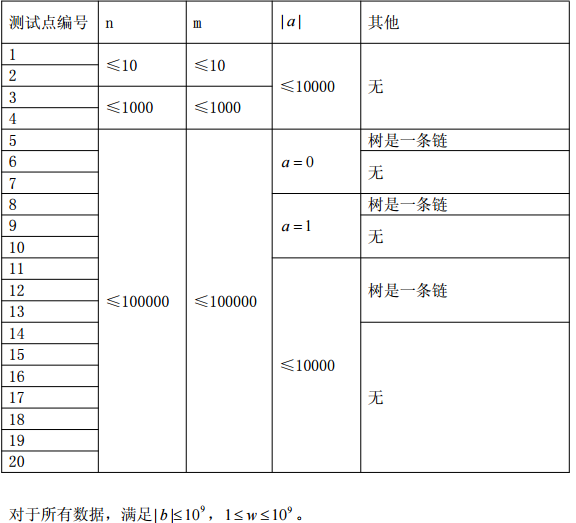传送门： http://www.lydsy.com/JudgeOnline/problem.php?id=4515

呜呜呜。没来得及交。

可是发现依旧标算写炸QAQ（代码能力爆负吧

树剖看上去应该挺明显的呀

至今未成功

求高人指点QAQ

WA飞了肿么办

/**************************************************************
    Problem: 4515
    User: lujiaxin
    Language: C++
    Result: Wrong_Answer
****************************************************************/
 
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <queue>
#define INF 133456789123456789
#define LL long long
#define NN 100010
using namespace std;
int n,m,type,numm=0,pos[NN],anc[NN],fa[NN][20],sz[NN],head[NN],son[NN];
int x,y,z,s,t,tot=0,deep[NN],id[NN];
LL a,b,minn[NN<<2],diss,dis[NN],A[NN<<2],B[NN<<2];
bool tag[NN<<2]={0};
struct E
{
    int ne,v,u; LL w;
}e[NN<<1];
int read()
{
    int xx; bool f=0; char CH;
    for (CH=getchar();CH<'0'||CH>'9';CH=getchar()) if (CH=='-') f=1;
    for (xx=0;CH>='0';CH=getchar()) xx=xx*10+CH-'0'; if (f) xx=-xx;
    return xx;
}
LL Read()
{
    LL xx; bool f=0; char CH;
    for (CH=getchar();CH<'0'||CH>'9';CH=getchar()) if (CH=='-') f=1;
    for (xx=0;CH>='0';CH=getchar()) xx=xx*10+CH-'0'; if (f) xx=-xx;
    return xx;
}
void Build(int xx,int yy,LL zz)
{
    e[++tot].ne=head[xx], head[xx]=tot, e[tot].v=yy, e[tot].u=xx, e[tot].w=zz;
    e[++tot].ne=head[yy], head[yy]=tot, e[tot].v=xx, e[tot].u=yy, e[tot].w=zz;
}
void DFS1(int xx)
{
    for (int i=1;i<=17;++i)
    {
        if (deep[xx]<(1<<i)) break;
        fa[xx][i]=fa[fa[xx][i-1]][i-1];
    }
    sz[xx]=1;
    for (int i=head[xx];i;i=e[i].ne)
    if (e[i].v!=fa[xx][0])
    {
        fa[e[i].v][0]=xx, deep[e[i].v]=deep[xx]+1, dis[e[i].v]=dis[xx]+e[i].w;
        DFS1(e[i].v);
        sz[xx]+=sz[e[i].v];
        if (sz[e[i].v]>sz[son[xx]]) son[xx]=e[i].v;
    }
}
void DFS2(int xx,int chain)
{
    pos[xx]=++numm, anc[xx]=chain, id[numm]=xx;
    if (son[xx]) DFS2(son[xx],chain);
    for (int i=head[xx];i;i=e[i].ne)
    if (e[i].v!=son[xx] && e[i].v!=fa[xx][0]) DFS2(e[i].v,e[i].v);
}
 
void push_up(int x,int l,int r)
{
    if(tag[x]) minn[x]=min(A[x]*dis[id[l]],A[x]*dis[id[r]])+B[x];  
    if(l!=r) minn[x]=min(minn[x],min(minn[2*x],minn[2*x+1]));
}
 
void Ins(int k,int l,int r,LL a,LL b)
{
    if (!tag[k]) { tag[k]=1, A[k]=a, B[k]=b, push_up(k,l,r); return;    }
    int mid=(l+r)>>1;
    LL xa=A[k]*dis[id[l]]+B[k], ya=A[k]*dis[id[r]]+B[k],xb=a*dis[id[l]]+b, yb=a*dis[id[r]]+b;
    if (xb<=xa && yb<=ya) { A[k]=a, B[k]=b;}
    else if (xb>=xa && yb>=ya) return;
    else
    if (a<A[k])
    {
        LL tmp=(b-B[k])/(A[k]-a)+1;
        if (tmp<=dis[id[mid]]) swap(a,A[k]), swap(b,B[k]), Ins(k<<1,l,mid,a,b);
        else Ins(k<<1|1,mid+1,r,a,b);
    }
    else
    {
        LL tmp=(b-B[k]-1)/(A[k]-a);
        if (tmp>dis[id[mid]]) swap(A[k],a),swap(B[k],b), Ins(k<<1|1,mid+1,r,a,b);
        else Ins(k<<1,l,mid,a,b);
    }
    push_up(k,l,r);
}
 
void Insert(int x,int l,int r,int _l,int _r,LL a,LL b){
    if(_l<=l&&r<=_r){
        Ins(x,l,r,a,b);    
    }
    else {
        int mid=(l+r)>>1;
        if(_l<=mid) Insert(2*x,l,mid,_l,_r,a,b);
        if(_r>mid) Insert(2*x+1,mid+1,r,_l,_r,a,b);    
    }
    push_up(x,l,r);
}
 
int LCA(int xx,int yy)
{
    if (deep[xx]<deep[yy]) swap(xx,yy);
    int tmp=deep[xx]-deep[yy];
    for (int i=0;i<=17;++i) 
        if (tmp&(1<<i)) xx=fa[xx][i];
    for (int i=17;i>=0;--i)
        if (fa[xx][i]!=fa[yy][i]) xx=fa[xx][i],yy=fa[yy][i];
    if (xx==yy) return xx;
    else return fa[xx][0];
}
LL Getmn(int k,int l,int r,int x,int y)
{
    if (l==x && r==y) return minn[k];
    int mid=(l+r)>>1;
    if (y<=mid) return Getmn(k<<1,l,mid,x,y);
    else if (x>mid) return Getmn(k<<1|1,mid+1,r,x,y);
    else return min(Getmn(k<<1,l,mid,x,mid),Getmn(k<<1|1,mid+1,r,mid+1,y));
}
LL Smin(int x,int f)
{
    LL mn=INF;
    while (anc[x]!=anc[f])
    {
        mn=min(mn,Getmn(1,1,n,pos[anc[x]],pos[x]));
        x=fa[anc[x]][0];
    }
    mn=min(mn,Getmn(1,1,n,pos[f],pos[x]));
    return mn;
}
void Change(int x,int f,LL a,LL b)
{
    while (anc[x]!=anc[f]) Insert(1,1,n,pos[anc[x]],pos[x],a,b), x=fa[anc[x]][0];
    Insert(1,1,n,pos[f],pos[x],a,b);
}
int main()
{
    n=read(), m=read();
    for (int i=1;i<=(n<<4);++i) minn[i]=123456789123456789ll;
    for (int i=1;i<n;++i) x=read(), y=read(), z=Read(), Build(x,y,z);
    memset(dis,0,sizeof(dis));
    DFS1(1), DFS2(1,1);
    while (m--)
    {
        type=read();
        if (type==1)
        {
            s=read(), t=read(), a=Read(), b=Read();
            int l=LCA(s,t),ss=s,tt=t;
            Change(s,l,-a,b+a*dis[s]);
            Change(t,l,a,b+a*(dis[s]-2*dis[l]));
        }
        else
        {
            s=read(), t=read();
            int l=LCA(s,t);
            printf("%lld\n",min(Smin(s,l),Smin(t,l)));
        }
    }
    return 0;
}